| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 다이나믹 프로그래밍
- algorithm
- 최소 신장 트리
- Longest Common Subsequence
- graph
- 플로이드 위셜
- prim
- 유니온 파인드
- 크루스칼
- 트리
- minimum spanning tree
- 우선순위 큐
- LCS
- 알고리즘
- 그래프
- 강한 연결 요소
- Strongly Sonnected Coponent
- 최단 거리
- 최소 스패닝 트리
- traceback
- 최단 경로
- 벨만 포드
- numpy
- 우선 순위 큐
- 넘파이
- 파이썬
- python
- 최장 공통 부분 수열
- tree
- priority queue
- Today
- Total
codinging
[알고리즘] MST(Minimum Spanning Tree) 최소 신장 트리, Kruskal, Prim Algorithm 알아보기 본문
[알고리즘] MST(Minimum Spanning Tree) 최소 신장 트리, Kruskal, Prim Algorithm 알아보기
대충사는사람1 2023. 5. 21. 18:08
MST
Spanning Tree 란 모든 노드를 포함하는 부분 그래프이다.
Minimum이 추가된 Minimum Spanning Tree 는 간선의 합이 가장 작고 모든 노드를 지나는 부분 그래프를 말한다.
Minimum Spanning Tree를 구하는 알고리즘은 Kruskal , Prim 알고리즘이 있다.
백준 1197
https://www.acmicpc.net/problem/1197
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
Kruskal Algorithm : O(ElogE)
모든 간선을 가중치 기준으로 오름차순으로 정렬해 Cycle이 없도록 간선을 순차적으로 선택하는 알고리즘이다.
Cycle 이 없도록 하려면 간선을 연결할때 두 노드가 이미 같은 집합이라면 포함하지 않고 같은 집합이 아니라면
포함 시키면 된다. Union Find 알고리즘을 통해 같은 집합인지 확인 가능하다.
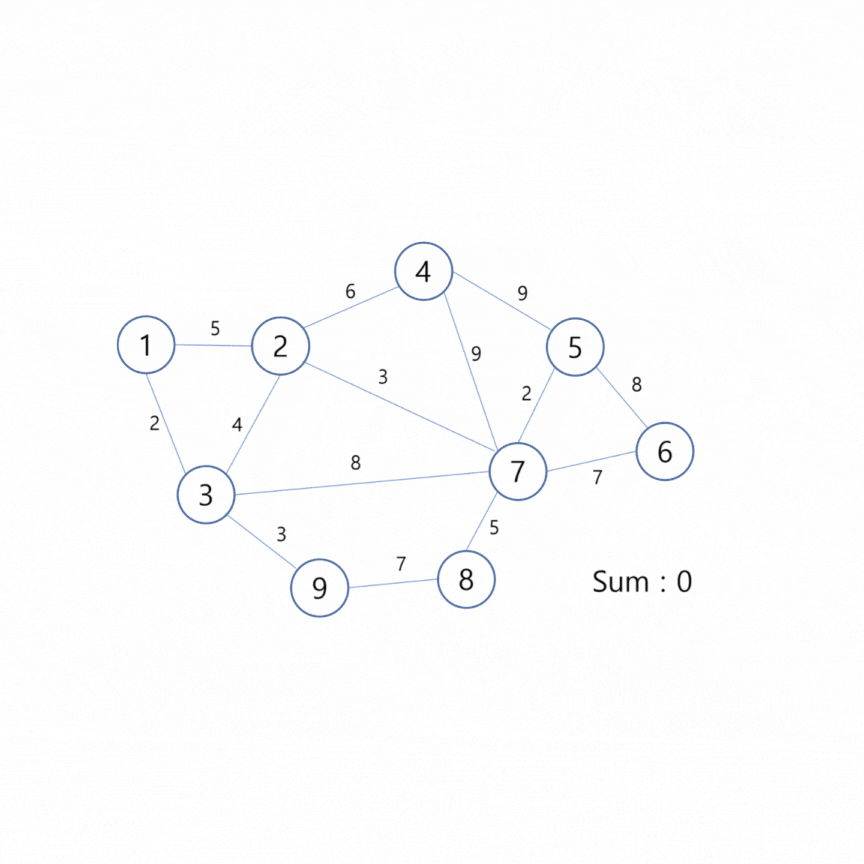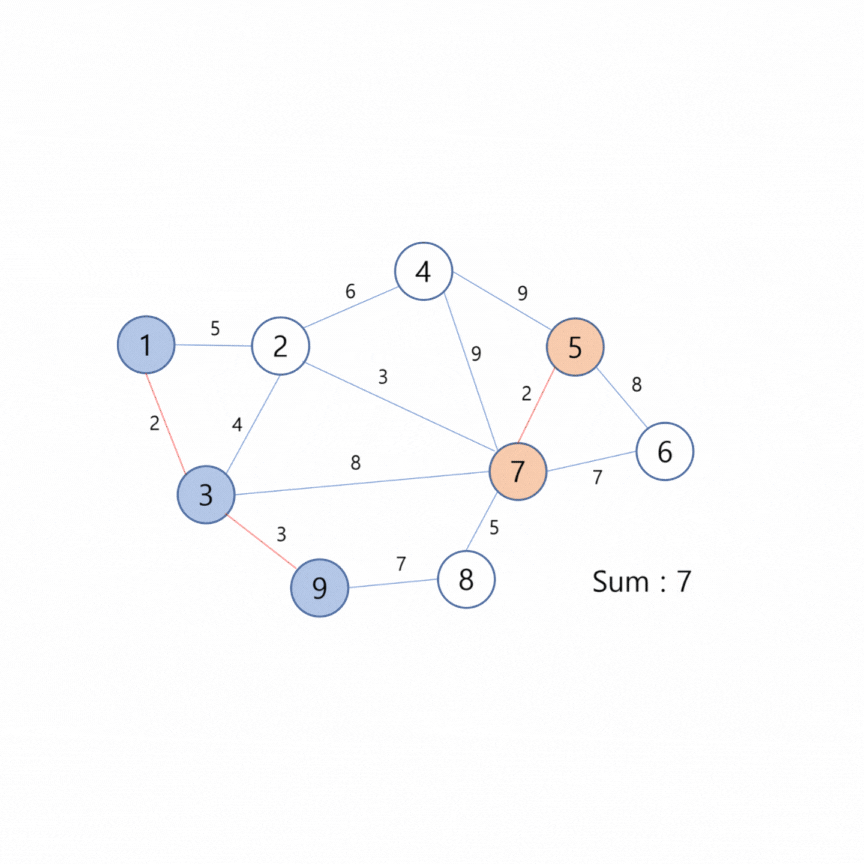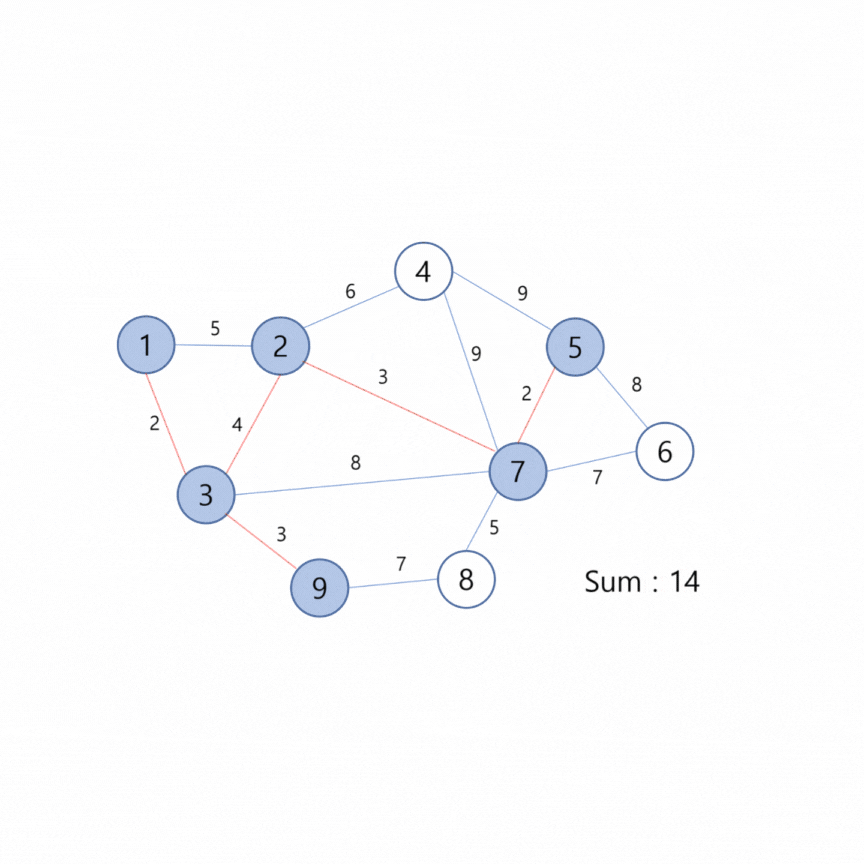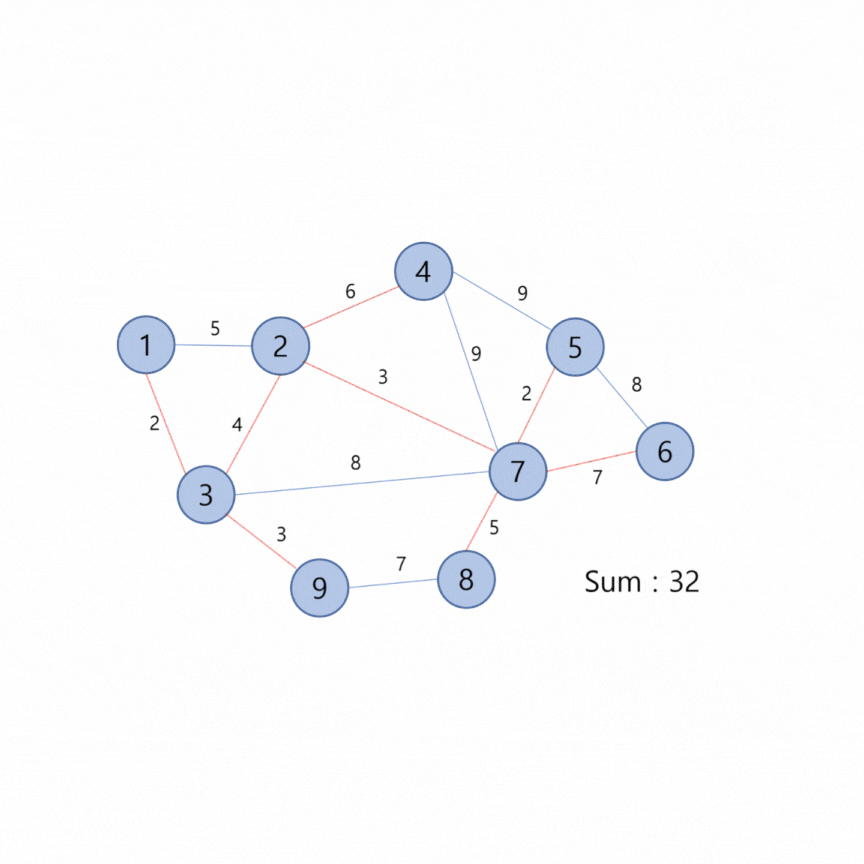
🦝 오름차순으로 정렬한다.
🦝 가장 낮은 가중치의 간선을 선택하고, Union Find 알고리즘을 통해 두 노드가 같은 그래프에 속한지 확인한다.
🦝 연결된 두 노드가 같은 그래프에 속해 있다면 다음 순서의 간선을 확인한다.
두 노드가 다른 그래프에 속해 있다면 두 그래프를 합친후 간선의 가중치를 합한다.
🦝 모든 노드를 연결할때 까지 반복한다.
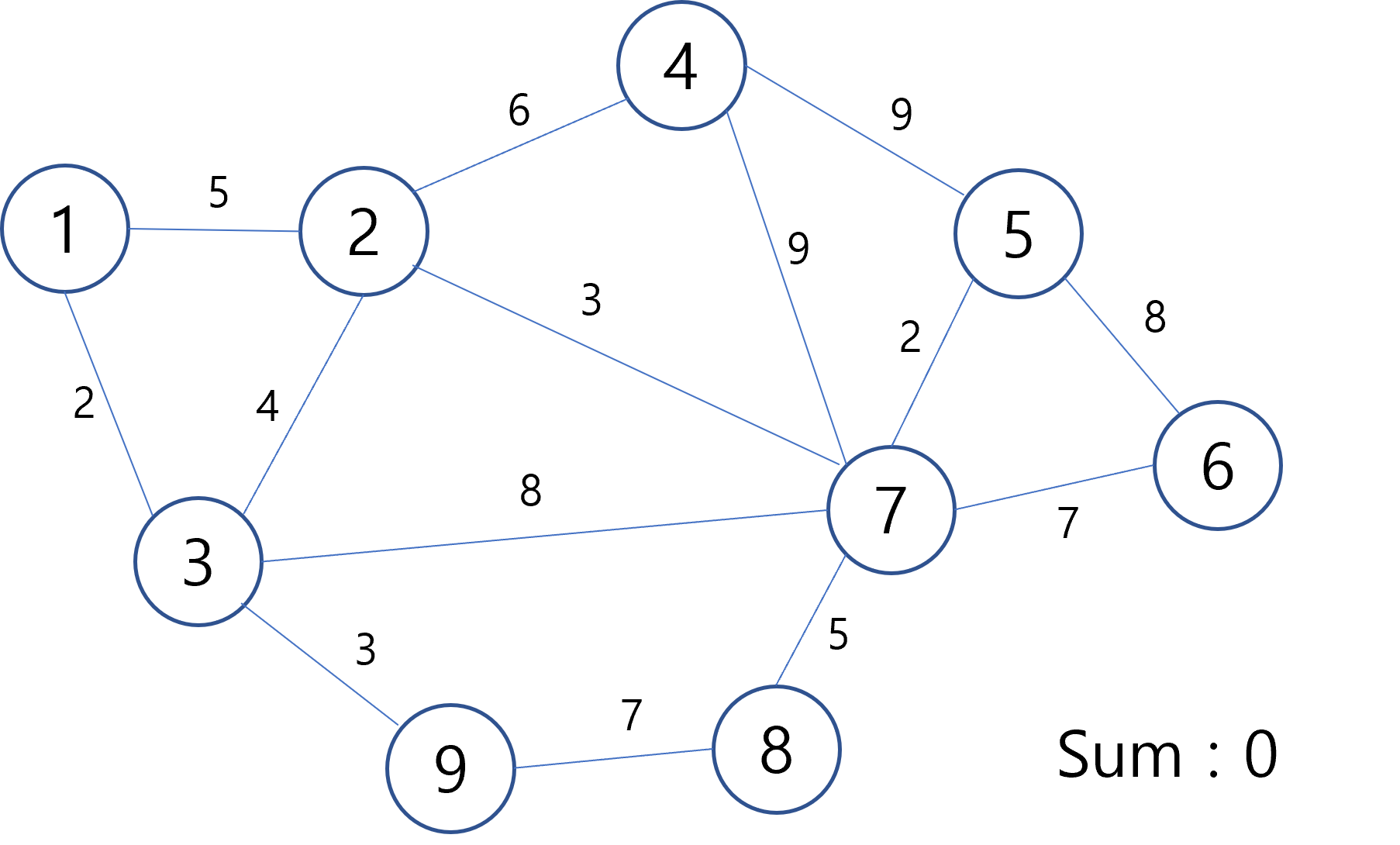
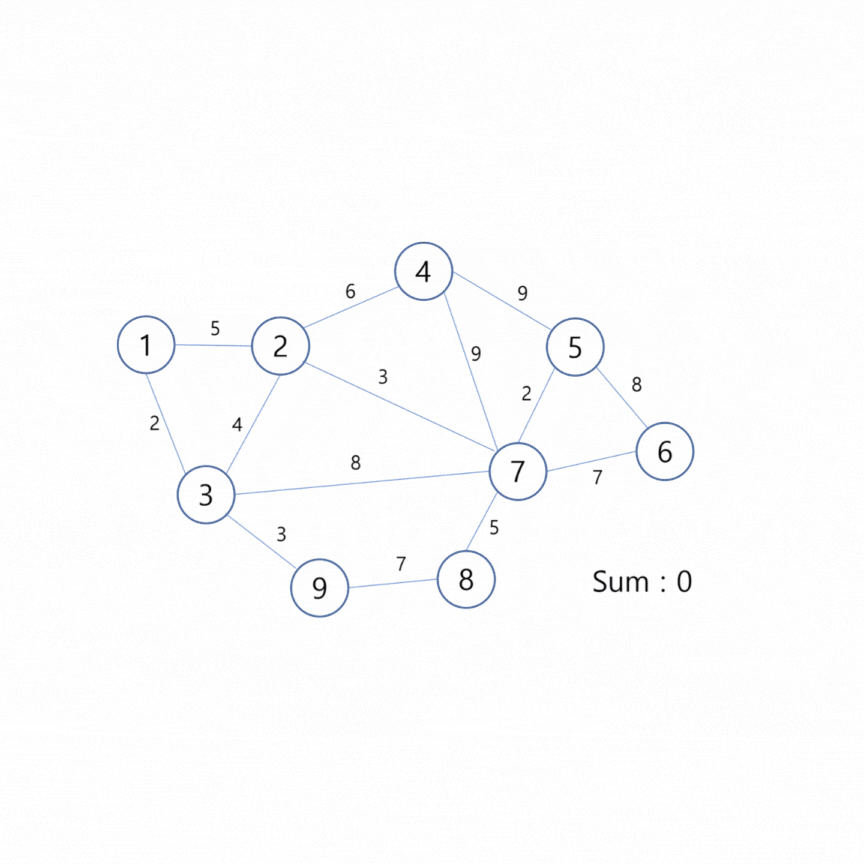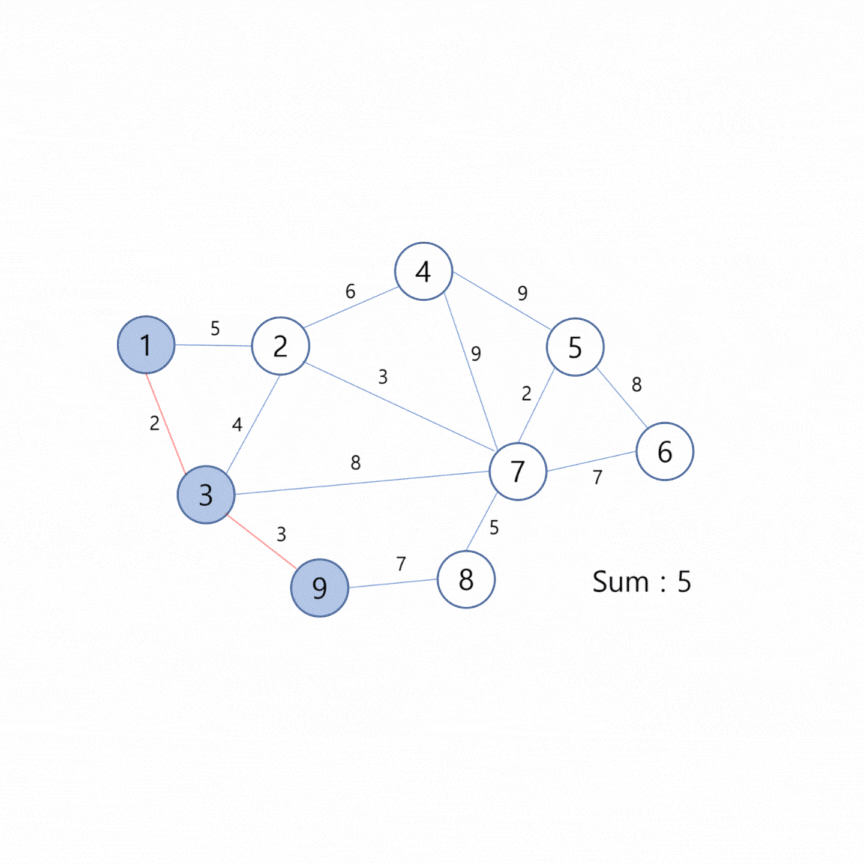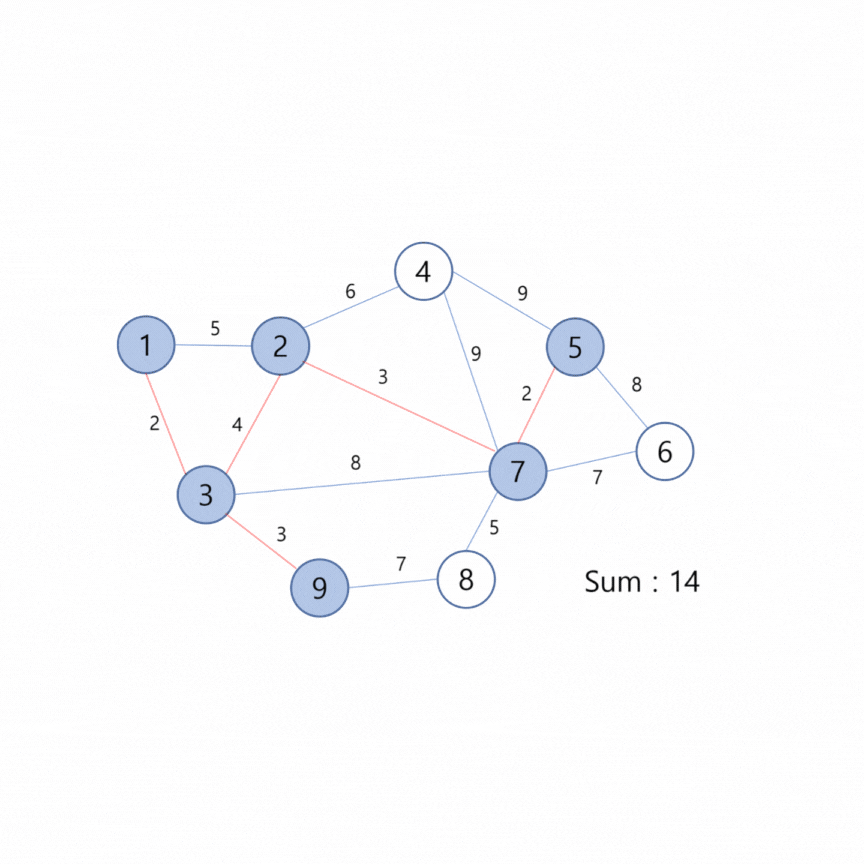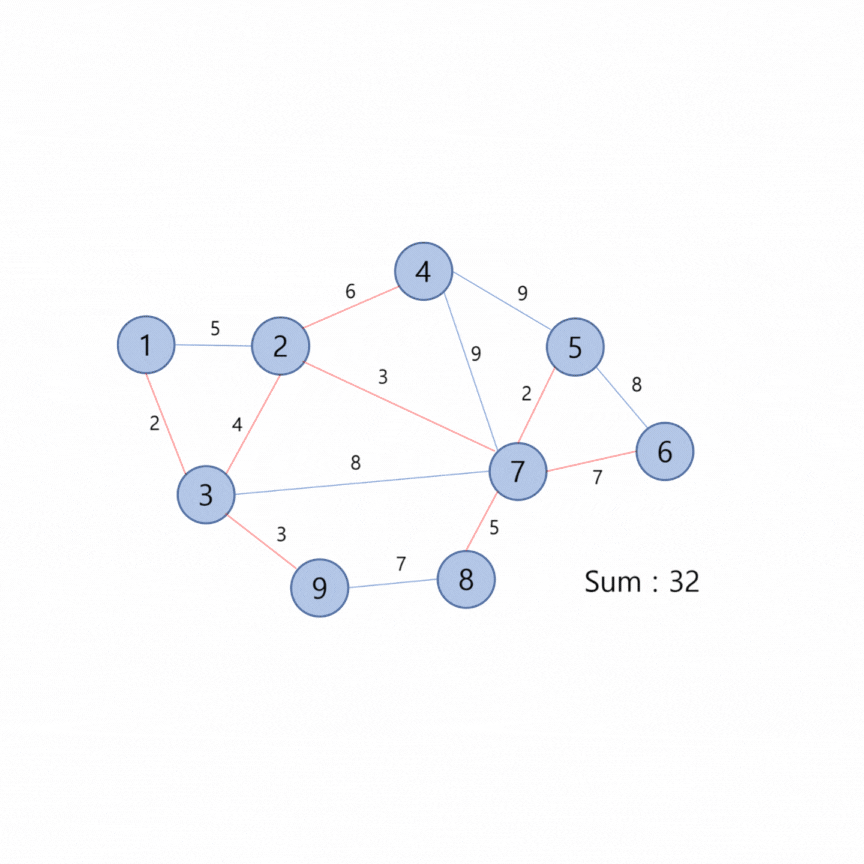
이 그래프를 이용해 Kruskal Algorithm 을 나타내면 다음과 같다.
코드
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX_V 10001
#define MAX_E 100001
int V, E, u, v, w;
int parent[MAX_V];
pair<int, pair<int, int>> edges[MAX_E];
int find(int x) {
if (x == parent[x]) return x;
return parent[x] = find(parent[x]);
}
void merge(int x, int y) {
x = find(x);
y = find(y);
if (x != y) parent[x] = y;
}
int kruskal() {
for (int i = 1; i <= V; i++) parent[i] = i; // union-find 전처리
sort(edges, edges + E); // 오름차순 정렬
int cnt = 0, ans = 0;
for (int i = 0; i < E; i++) {
u = edges[i].second.first;
v = edges[i].second.second;
w = edges[i].first;
// 같은 집합이 아닐시 간선 선택
if (find(u) != find(v)) {
merge(u, v);
ans += w;
cnt++;
if (cnt == V - 1) break;
}
}
return ans;
}
int main() {
cin >> V >> E;
for (int i = 0; i < E; i++) {
cin >> u >> v >> w;
edges[i] = make_pair(w, make_pair(u, v));
}
cout << kruskal() << endl;
return 0;
}Prim Algorithm : O(ElogV)
한 노드에서 시작해 정점을 집합에 추가해 나가는 방식을 가지고 있다.
🦝 선택된 노드를 MST 집합에 넣는다.
🦝 MST 집합의 노드 중 에서 연결된 간선중 가장 작은 가중치의 간선에 연결된 노드를 MST 집합에 포함 시킨다.
( 이때 선택한 노드가 이미 MST 집합에 속해 있다면 다음 간선을 선택한다. )
🦝 위의 단계를 모든 노드가 선택될 때 까지 반복한다.
코드
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
#define MAX_V 10001
typedef pair<int, int> pair_ii;
int V, E, u, v, w;
bool visit[MAX_V];
vector<pair_ii> graph[MAX_V];
priority_queue<pair_ii, vector<pair_ii>, greater<pair_ii>> pq;
long long prim() {
long long ans = 0;
pq.push(make_pair(0, 1)); // 선택된 가중치, 노드 저장
while (!pq.empty())
{
int now_weight = pq.top().first;
int now_node = pq.top().second;
pq.pop();
// 방문 확인
if (visit[now_node]) continue;
visit[now_node] = true; // 방문 표시
ans += now_weight;
// 연결 노드들 우선순위 큐에 삽입
for (int i = 0; i < graph[now_node].size(); i++)
{
int next_node = graph[now_node][i].first;
int next_weight = graph[now_node][i].second;
pq.push(make_pair(next_weight, next_node));
}
}
return ans;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> V >> E;
for (int i = 0; i < E; i++)
{
cin >> u >> v >> w;
graph[u].push_back(make_pair(v, w));
graph[v].push_back(make_pair(u, w));
}
cout << prim(); << '\n';
}
'Algorithm' 카테고리의 다른 글
| [알고리즘] 최단 경로 알고리즘 다익스트라(Dijkstra) 알아보기 (0) | 2023.07.10 |
|---|---|
| [알고리즘] Union Find 알아보기 (1) | 2023.05.06 |
| [알고리즘] 강한 연결 요소(Strongly Connected Component, SCC) 알아보기 (0) | 2023.04.09 |
| [알고리즘] LCS(Longest Common Subsequence) 최장 공통 부분 수열 과 역추적(Trace Back) 알아보기 (1) | 2023.03.31 |




