| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Longest Common Subsequence
- 최소 신장 트리
- 다이나믹 프로그래밍
- graph
- 플로이드 위셜
- 최단 경로
- 그래프
- python
- algorithm
- LCS
- prim
- 넘파이
- 최단 거리
- minimum spanning tree
- 벨만 포드
- 크루스칼
- numpy
- traceback
- 최장 공통 부분 수열
- Strongly Sonnected Coponent
- 유니온 파인드
- priority queue
- 우선 순위 큐
- 강한 연결 요소
- tree
- 트리
- 최소 스패닝 트리
- 알고리즘
- 우선순위 큐
- 파이썬
- Today
- Total
codinging
[알고리즘] LCS(Longest Common Subsequence) 최장 공통 부분 수열 과 역추적(Trace Back) 알아보기 본문
[알고리즘] LCS(Longest Common Subsequence) 최장 공통 부분 수열 과 역추적(Trace Back) 알아보기
대충사는사람1 2023. 3. 31. 18:08
LCS 알고리즘
두 수열 사이에 공통적으로 존재하는 가장 긴 부분 수열을 말한다.
예를 들면 ABCDEF 와 EBDEAF 의 가장 긴 부분수열은 BDEF 이다.
설명
문자열 X[i] = {x1, x2, x3 . . .xi} , Y[j] = {y1, y2, y3 . . .yj} 인 두 문자열이 있다, 그리고 이 두 문자열의 LCS의 길이를 구하는 함수를 LCS_LEN(X[i], Y[j]) 라고 하자
🐧첫번째 경우( i == 0 )
만약 i == 0 이라면 문자열의 길이가 0이라는 뜻이니 LCS_LEN(X[i], Y[j]) == 0 이다.
🐧두번째 경우( xi == yj )
X[i] 문자열의 i번째 문자 xi 와 Y[i] 문자열의 j번째 문자 yj 가 같다( xi == yj ) 라면 다음과 같은 식이 성립한다.
LCS_LEN(X[i], Y[j]) = LCS_LEN(X[i - 1], Y[j - 1]) + 1
예를 들면 x[i] = ABCDEF , y[j] = EBDEAF 이라고 할때 x[i - 1] = ABCDE , y[j - 1] = EBDEA 이다.
당연하게도 ABCDE 와 EBDEA 의 LCS를 구하는 LCS_LEN(X[i - 1], Y[j - 1]) == 3 일 것이고,
x[i -1], y[j - 1] 에서 마지막에 'F' 가 추가된 ABCDEF 와 EBDEAF 즉 x[i], y[j] 의 LCS_LEN() 은
LCS_LEN(X[i], Y[j]) = LCS_LEN(X[i - 1], Y[j - 1]) + 1 라는 식이 성립 하게 된다.
🐧세번째 경우(xi != yj)
xi 와 yj 가 다른 경우다. 이 경우 LCS_LEN(X[i], Y[j]) 는 바로 한 단계 전인
LCS_LEN(X[i], Y[j - 1]), LCS_LEN(X[i - 1], Y[j]) 중 큰 값을 가진다.
세 가지 경우를 정리하여 다음 점화식을 만들수 있다.
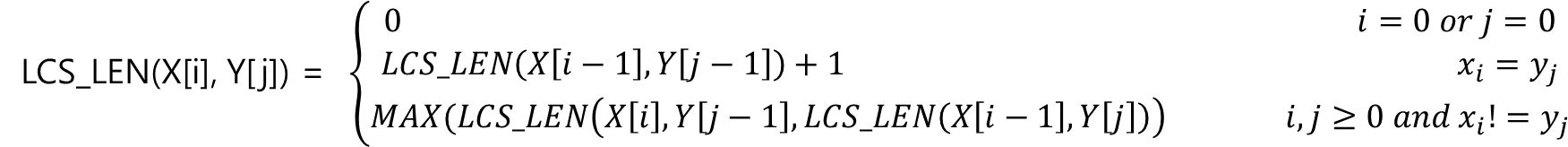
점화식을 다음과 같이 정리 할 수 있다.
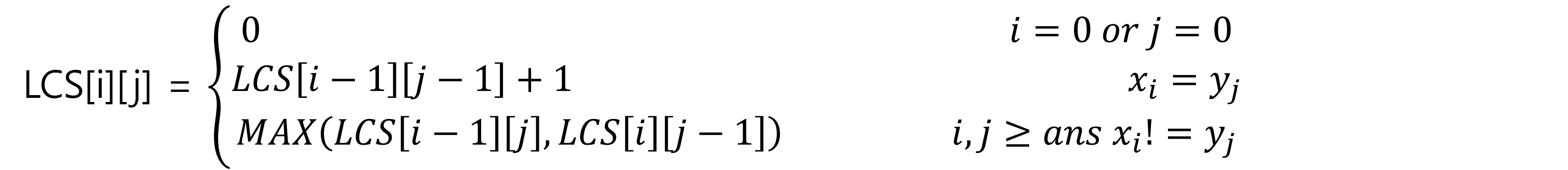
구현

dp로 구현한 lcs 알고리즘
#include <iostream>
#include <algorithm>
using namespace std;
int lcs[1001][1001];
void LCS(string s1, string s2) {
int len1 = s1.size();
int len2 = s2.size();
for (int i = 0; i < len1; i++) {
for (int j = 0; j < len2; j++) {
if (i == 0 || j == 0) {
lcs[i][j] = 0;
continue;
}
if (s1[i] == s2[j])
lcs[i][j] = lcs[i - 1][j - 1] + 1;
else
lcs[i][j] = max(lcs[i - 1][j], lcs[i][j - 1]);
}
}
cout << lcs[len1 - 1][len2 - 1] << '\n';
}LCS 역추적 알고리즘
lcs 알고리즘은 두 문자열의 lcs 길이를 구하는 함수다.
하지만 역추적 함수를 구현해 lcs의 요소, 즉 lcs 그 자체를 구할 수 있다.
설명
다음은 lcs를 역추적 하는 과정이다. lcs 의 문자열을 ans 라고 하겠다.
🐧 0 . 제일 오른쪽 아래 에서 시작한다.
🐧 1 . 현재 위치한 값이 위쪽(↑, i - 1) 과 값이 같으면 현재 인덱스의 문자를 ans에 저장 후 위로 이동
🐧 2 . (1번에 만족하지 않고) 현재 위치한 값이 왼쪽(←, j - 1) 과 값이 같으면 현재 인덱스의 문자를 ans에 저장 후
왼쪽 으로 이동한다.
🐧 3 . 현재 위치한 값이 대각 위(↖, i - 1 , j - 1) 보다 크면(1번, 2번 조건이 만족하지 않을때 ) 현재 인덱스의 문자를 ans에 저장 후
대각 위(↖) 로 이동한다.
🐧 4 . i == 0 또는 j == 0 이 될때까지 1, 2, 3번을 반복한다.
1번과 2번을 바꿔도 상관없다.
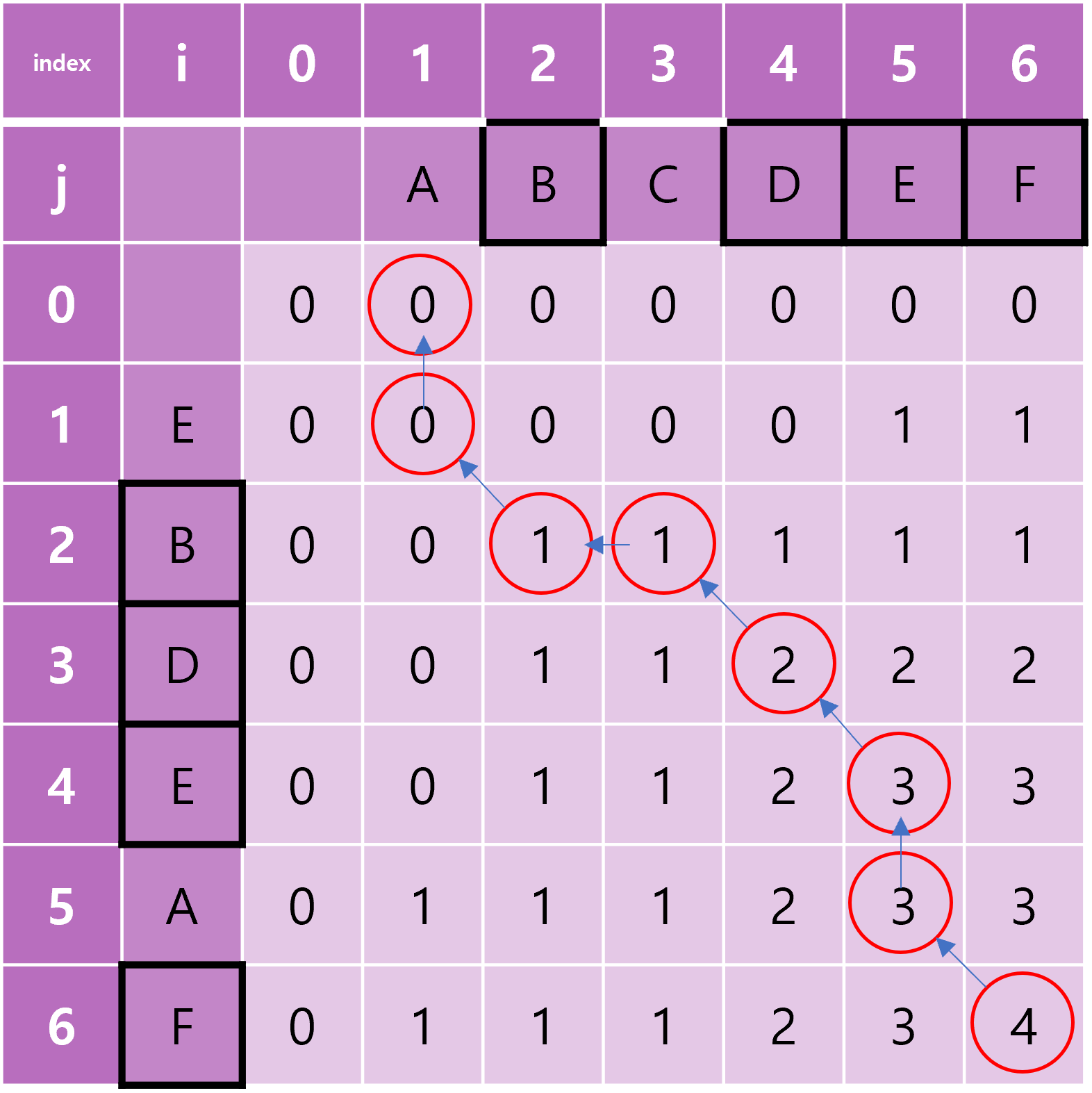
🐧 5 . ans 에는 FEDB 가 저장 되어 있을 것 이다. 이것을 역전 시켜주면 BDEF 라는 lcs가 나오게 된다!
구현
#include <iostream>
#include <algorithm>
using namespace std;
int lcs[1001][1001];
void TRACE_BACK(string s1, string s2) {
string ans;
int i = s1.size() - 1;
int j = s2.size() - 1;
while (1) {
if (i == 0 || j == 0)
break;
if (lcs[i][j] == lcs[i][j - 1])
i -= 1;
else if (lcs[i][j] == lcs[i - 1][j])
j -= 1;
else {
ans += s1[i];
i -= 1;
j -= 1;
}
}
reverse(ans.begin(), ans.end());
cout << ans;
}
🐧추천 문제🐧
백준 9252
https://www.acmicpc.net/problem/9252
9252번: LCS 2
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
www.acmicpc.net
'Algorithm' 카테고리의 다른 글
| [알고리즘] 최단 경로 알고리즘 다익스트라(Dijkstra) 알아보기 (0) | 2023.07.10 |
|---|---|
| [알고리즘] MST(Minimum Spanning Tree) 최소 신장 트리, Kruskal, Prim Algorithm 알아보기 (2) | 2023.05.21 |
| [알고리즘] Union Find 알아보기 (1) | 2023.05.06 |
| [알고리즘] 강한 연결 요소(Strongly Connected Component, SCC) 알아보기 (0) | 2023.04.09 |




